Appendices

Appendix A.
New Features

New Features of Version 3.4 --- June, 1996

• The fast RF can now be used for any Euler angle conventions or even polar angles. The program will do interpolation if necessary.
• Bug fix in ORFLRF for the interpolation.

New Features of Version 3.3 --- April, 1996

• Calculation of fast rotation functions with normalized structure factors is supported. New command NORMalize.
• Calculation of the self rotation function in polar angles with the fast RF, by interpolation.
• Correlation of ordinary cross RF results with the self RF. New command XCORrelate.
• Bug fixes and documentation updates.

New Features of Version 3.2 --- September, 1995

• A general locked translation function is implemented. A new command GLTF is introduced.
• The program can automatically carry out fine searches, with the slow rotation function, for the top peaks of the RF. A new command PKFIt is implemented. These fine search results are used by P1PC and GLTF commands.
• An option of calculating the locked RF by interpolating among ordinary slow RF values is implemented. A new command LOCInterpolate is introduced.
• The program will select both Ca and P atoms for packing check in the locked translation function.
• Modified the coordinate I/O routines to fully support the PDB format.
• Implemented a new orthogonalization convention, CXCAZ.
• Various bug fixes.
• Updated the documentation.

New Features of Version 3.1 --- June, 1995

• The Patterson correlation refinement of ordinary cross RF peaks is now possible. The correlation that is maximized is different from that used in X-Plor. New commands COORdinate, GROUp, and P1PC.
• The Crowther fast rotation function is now fully implemented. It can be used to calculate locked as well as ordinary self or cross rotation functions.
• The unique rotational space for Eulerian searches can be assigned automatically for ordinary self and cross RF (a special feature of the command SLIMits). The program can also try to assign the limits for the locked RF.
• A new algorithm for the calculation of the slow RF is implemented, which will determine RCUTLO (command RCUToff) automatically and can lead to a three-fold speed-up. The implementation of RCUTHI (command RCUToff) has been changed.
• A new definition of the locked cross RF is used, which should simplify the definition of the unique rotational space.
• FFT routines have been incorporated to perform the transform from calculations done with the command TFUNction directly.
• The angles in the peak listing in the print file are now labeled. The three coordinate axes in the stereographic projection are labeled with the approapriate unit cell axis.
• Bug fixes.
• Updated the documentation.

Appendix B.
Example Inputs

Example input files to this program are provided together with the program distribution. This appendix shows examples for blocks of related inputs. The required portion of each command is given in upper case.

General Set-up
TITLe RF calculation
COMMent anything goes here
PRINt glrf.prt
EULEr zxz
POLAr xzk
ORTHogonalization axabz

Define Crystal A
ACELl 90 90 90 90 90 90
ASYMmetry p212121
AOBS-file fobs.dat
AFORmat 3i4, 2f8.2
ACUToff 1 1 0
APOWer 2
NSHEll 8
ORIGin true

Slow Self Rotation Function
SELF true
CROSs false
FAST false
CUTOff 1.5
BOXSize 3 3 3
GEVAluation 2
RADIus 20
RESOlution 10 3.5
SANGle polar
OANGle euler zxz
SLIMits 1 0 180 3
SLIMits 2 0 180 3
SLIMits 3 180 180 2
MAPFile srf.map

Fast Cross Rotation Function
SELF false
CROSs true
FAST true
RADIus 30
RESOlution 10 3.5 \
CUTOff 0.2
SANGle euler
OANGle euler zxz
SLIMits 270 270 0 \
MAPFile xrf.map

Peak Search and Fitting
PEAK 3 50
PKFIt 4 1.5

Contour Plots
CNTFile glrf.ps
CNTLevel 500 1000 50
SECTion 123

Read in Old Map File
PEAK 3 30 glrf.map
CNTFile glrf.ps
CNTLevel 500 1000 50
SECTion 123

Patterson Correlation Refinement
COORdinate input model.pdb
COORdinate boverall 30
COORdinate output rigid.pdb
GROUp 1 1 60
GROUp 1 181 250
GROUp 2 61 180
P1PC 10 5 1.5

Real Space Rotation Function
RSRF rotation 20 30 40 search
RSRF a-center 0.1 0.2 0.3
RSRF b-center 0.4 0.6 0.5

Non-crystallographic Symmetry
LOCSymmetry 1 0 0 2 vector
LOCSymmetry 1 1 1 3
LOCExpand true

Fast Locked Cross RF
LOCSymmetry 1 0 0 2 vector
LOCSymmetry 0 1 0 2 vector
LOCExpand true
LOCOrient 10 20 30 euler
SELF false
CROSs true
FAST true
RADIus 30
RESOlution 10 4
CUTOff 0.2
SANGle euler
OANGle euler zyz
SLIMits 1 0 180 3
SLIMits 2 0 90 3
SLIMits 3 0 360 3

Locked Translation Function
COORdinate input model.pdb
COORdinate boverall 30
COORdinate output gltf.pdb
GLTF cutoff 1.5
GLTF direct false
GLTF overlap 10 3
GLTF packing false
GLTF radius 30
GLTF rfpeak 10
GLTF SLIMits 1 -30 30 1
GLTF SLIMits 2 -30 30 1
GLTF SLIMits 3 -30 30 1

Appendix C. 
The Triple Rotation Function

In many cases a protein sample has been crystallized into two (or more) different space groups. The orientational relationship between a molecule in the first crystal form and one in the second can be determined by a cross-rotation function between the two crystal forms. Thus, we have the following relationship,

where the two crystal forms are called B and C. Now a cross rotation function can be calculated between a search model and crystal forms B and C simultaneously. The two individual rotation functions are,

Noting the relationship between the B and the C crystals, we should have

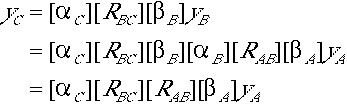
Therefore,

The cross-locked rotation function (or triple rotation function) can be defined as the product of the rotation function values corresponding to matrix $[R_{AB}]$ between A and B crystal and matrix $[R_{BC}] [R_{AB}]$ between A and C crystal.

The above derivation can be easily generalized to cases where there are more than one rotational relationships between crystals B and C, and to cases where there are more than two crystal forms (quadruple rotation function ...).

Appendix D.
The Real Space Rotation Function

This function is defined as the product of the electron density for two copies of the same molecule. It is dependent on both the rotational and the translational relationship between the two copies (and in this sense the function is more than just a rotation function).

The relationship between the two copies of the molecule can be written as,

If $S_A$ and $S_B$ are the centers of the molecule in crystals A and B, respectively, then

The correlation between the two molecular copies should be a function of $[C], S_A$ and $S_B$,