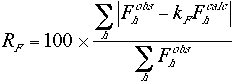
(1)
Translation searches are employed to determine the location of molecules (with known orientations) in a crystal unit cell. The search is normally formulated as a minimization or maximization of certain indicators by varying the positional parameters of the molecules in the unit cell. Most indicators involve a comparison between the observed and the calculated structure factor amplitudes. For example, the difference between the observed and the calculated structure factor amplitudes (or the R factor) can be minimized. Alternatively, the correlation between the observed and the calculated structure factor amplitudes can be maximized.
A. THE R FACTOR AND THE CORRELATION COEFFICIENT
The crystallographic R factor is often used as an indicator in translation searches. It is a measure of the percentage difference between the observed and the calculated structure factor amplitudes,
|
|
(1) |
A similar R factor can be defined based on the square of the structure factor amplitudes, i.e., an R factor based on intensity,
|
|
(2) |
In the equations above kF and kI are scale factors that bring the observed and the calculated structure factors to the same level,
|
|
The scale factors are calculated in shells of equal reciprocal volume. This will compensate for any differences in the temperature factors between the observed and the calculated structure factor amplitudes. The R factor values are very sensitive to the position and the orientation of the molecules in the unit cell. The correlation coefficients between the observed and the calculated structure factors are somewhat less sensitive. Hence they may allow for larger errors in the reflection data as well as in the orientational parameters of the molecules. As is the case with the R factors, the correlation coefficients can be defined based on the amplitude or the intensity of the reflections.
|
|
(3) |
|
|
(4) |
In the equations N is the number of reflections that are used in the calculation. Unlike the R factors, the correlation coefficients do not depend on the overall scale factor between the observed and the calculated structure factors.
The region of the unit cell that should be covered for a translation search with the above indicators does not normally correspond to the asymmetric unit of the space group. Because the molecule to be searched has a determined orientation, it can only reside in one of the asymmetric units in the unit cell. Lacking a knowledge as to which asymmetric unit the molecule is occupying, the entire unit cell would need to be searched. However, most space groups have alternative origins, which means the position of a molecule in the unit cell can only be determined to within certain sets of translations (the Cheshire group). For example, in space group {\it P}\/2$_1$2$_1$2$_1$, there are eight alternative origins, at $(0, 0, 0)$, $(1/2, 0, 0)$, $(0, 1/2, 0)$, $(0, 0, 1/2)$, $(1/2, 1/2, 0)$, $(1/2, 0, 1/2)$, $(0, 1/2, 1/2)$, and $(1/2, 1/2, 1/2)$. This implies the region that should be searched to locate a molecule need only be 1/8 of the volume of the unit cell (for example, $[1/2, 1/2, 1/2]$). Once the first molecule has been located, the origin is determined as well. The search for subsequent molecules will need to cover the entire unit cell.
B. CALCULATION OF STRUCTURE FACTORS
In order to calculate $R$ factors and correlation coefficients for a translation search, structure factors need to be calculated for molecules at different positions in the unit cell. The orientations of the molecules have been determined beforehand with rotation searches (e.g., with the program GLRF). Therefore, only the positional parameters of the molecules need to be varied.
The structure factor equation can be written as a double summation --- first over the atoms in one asymmetric unit of the unit cell and then over all the asymmetric units,
|
|
(5) |
where j goes over all the atoms in the asymmetric unit and n goes over all the asymmetric units. The nth crystallographic symmetry operator is given by
|
|
|
|
where [Tn] is the rotational component and t n the translational component of the symmetry operator. For simplicity, consider the case where there is only one molecule in the asymmetric unit. In the translation search, the molecule will be placed at different positions in the unit cell,
|
|
|
(6) |
where x0 is a translation vector which relates the molecule located at x j with that located atxj0. Substituting x j in Eq. (6) into Eq. (5),
|
|
(7) |
here $f_{h, n}$ is the structure factor calculated based on the nth symmetry-related molecule only,
|
|
(8) |
Therefore, the summation over the atoms in the structure factor calculation, a rather time-consuming process, need to be performed only once, for the molecule at a reference position (xj0). Subsequent structure factor calculation after translation of the molecule from the reference position is no longer dependent on the number of atoms present in the unit cell (Eq. (7)).
The reference position is usually chosen with the center of the molecule at (0, 0, 0). Then the translation vector that is determined from the translation searches will define the center of the molecule in the unit cell.
Equation (7) can be generalized to allow for the presence of other molecules that are to remain stationary during the translation search,
|
|
(9) |
where Ah is the contribution from the stationary molecules. This formulation is useful if there are more than one molecules in the asymmetric unit. The position of one of the molecules can be determined first and the model is then input as a stationary molecule for the search of the position of the next molecule.
C. PATTERSON-CORRELATION TRANSLATION FUNCTION
Besides the R factor and the correlation coefficient, another commonly-used translation search indicator is the correlation between the observed and the calculated Patterson maps. Rotation functions are based on the overlap of only a subset of the interatomic vectors in the Patterson map, i.e. only the self-vectors within each crystallographically-unique molecule. The correct orientation and position of a molecular structure in the crystal unit cell should lead to the maximal overlap of both the self and the cross vectors, i.e. maximal overlap between the observed and the calculated Patterson maps throughout the entire unit cell,
|
|
(10) |
Note that the integral
![]()
is 1 when h +p = 0 and 0 otherwise.
The calculated structure factor is a function of the translation vector x0 (Eq. (9)). Combining Eqs. (9) and (10),
|
|
(11)
(12) |
The first two terms in Eq. (11) contribute a constant to the correlation and hence are omitted from further calculation. It can be seen from Eq. (11) that reflections (h, k, $\ell$) and (-h, -k, $-\ell$) contribute equally to the correlation. The translation function is therefore a Fourier transform, with h [Tn] and h [Tn]- [Tm]as the indices and the coefficients of this transform are defined by Eq. (12).
Sometimes it may be desirable to use a subset of the symmetry-related molecules in the translation function calculation. For example, in space group {\it P}\/4$_1$2$_1$2, molecules at (x, y, z ) and (-x, -y, 1/2+z ) can be used in the calculation. The translation function Fourier transform will have `reflections' with indices $(2h, 2k, 0)$, hence only the z =0 section need to be calculated. More importantly, the resolution of the translation function transform in this case is twice that of the reflection data used in the structure factor calculation.
The intra-molecular vectors can be removed from the observed Patterson map by subtracting the structure factors calculated from individual symmetry-related molecules (Eq. (8)) from the observed structure factors,
![]() ,
,
where k is a weighting factor on the intra-molecular vectors.
It has been suggested that only the phases, rather than both the phases and the amplitudes, of the calculated structure factors be used in the translation function calculation (Eq. (12)).
D. ELECTRON-DENSITY-CORRELATION (PHASED) TRANSLATION FUNCTION
If an atomic model needs to be placed in an electron density map that has been obtained through other methods (e.g., the MIR method or partial model phases), the electron density correlation translation function (also known as the phased translation function) can be used. It is defined as the product of the observed and the calculated electron density functions integrated over the unit cell. The derivation of the function is similar to that of the Patterson correlation translation function.
|
|
(13) |
Therefore the phased translation function is also a Fourier transform.